Алгоритми розгалуження мовою Pascal

Практична робота 1. 

Задачі на програмування. 

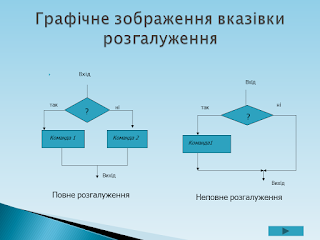
Алгоритми розгалуження.

Задача 1. Василько та Юлія грають в таку гру. Спочатку кожен записує на папері свій прогноз – число від 1 до 6. Потім вони кидають гральний кубик з числами від 1 до 6 на гранях. Чий прогноз виявляється ближчим до того числа, що випало, той і переміг. Треба написати програму для визначення переможця.

Технічні умови. Програма Forа  читає з пристрою стандартного введення три числа через пропуски (пробіли) – прогноз Василька, Юлі та результат кидання кубика. Програма виводить “V”, якщо переміг Василько, “J” якщо Юлія або ”D” – якщо прогноз обох однаково близький до результату (тобто переможця виявити неможливо.

Програма мовою Pascal

program fora;                                               {оголошення назви алгоритму}

var a,b,c : integer;                            {оголошення змінних цілих величин  a,b,c}

begin  writeln;                              {оголошення початку роботи алгоритму}

readln(a);  readln(b);  readln(c);      {оголошення про введення величин  a, b, c}

if ( (abs(c-a)) > (abs(c-b)) )  then write('j');  {якщо | c-a |>| c-b |, тоді написати j}

if ( (abs(c-a)) < (abs(c-b)) )  then write('v'); {якщо | c-a |>| c-b|, тоді написати v}

if ( (abs(c-a)) = (abs(c-b)) )  then write('d'); {якщо | c-a |>| c-b|, тоді написати  d}

end.

Протестувати алгоритм на правильність на прикладах:

1)Введення    3  4  5  Виведення J; 2) Введення: 1  6  2 Виведення  V; 3) Введення: 4  4  3 Виведення  D;  4)Введення    6  5  2  Виведення J;  5) Введення: 1  6  2  Виведення  V.

Завдання 2. Відомо, що книжкова полиця вміщає k однакових товстих книг, але k+1-а книга вже не влазить. Так само на неї можна поставити m однакових тонких книг, а m+1 -а вже не влізе. Скласти алгоритм, який знаходить можливість, щоб на полиці помістилися одночасно: n товстих та p тонких книг.

Розв’язання.  Якщо числовий вираз  n/k + p/m <=1, то можна, якщо  числовий  n/k + p/m > 1, то не можна помістити одночасно книги на полицю.

Алгоритм мовою Pascal (використовує повне розгалуження, «якщо-то, інакше»)

program BIBLIO;    var k,m,n,p,h:real;    begin

writeln('введіть число товстих книг 2<k<10⁹  k='); readln(k);

writeln('введіть число тонких книг 2<m<10⁹  m='); readln(m);

writeln('введіть даних товстих книг 2<n<10⁹  n='); readln(n);

writeln('введіть даних тонких книг 2<p<10⁹  p='); readln(p);  h:=(n/k)+(p/m);

 if  (h<1) or (h=1) then write(' кнгиги можна помістити') {розгалуження для виводу результату}

else  write('не можна помістити книги');  {інакше то вивід результату не можна} writeln('h=', h); end.

Протестувати алгоритм на правильність на прикладах:

1)Введення    3  4  5  6  Виведення ? 2) Введення: 1  6  2 8 Виведення  ?; 3) Введення: 4  4  3 9 Виведення  ?;  4)Введення    6  5  2  10  Виведення  ?;  5) Введення: 2  6  7  9  Виведення  ?

Завдання 3. Самостійно скласти і реалізувати алгоритм впорядкування виразів: (n/k)+(p/m)-(m/p)-(k/m); та (р/k)+(n/m)-(k/n)-(n/p) в порядку зростання для дробових чисел k,m,n,p.

Протестувати алгоритм на правильність на прикладах:

1)Введення    3  4  5  6  Виведення ? 2) Введення: 1  6  2 8 Виведення  ?; 3) Введення: 4  4  3 9 Виведення  ?;  4)Введення    6  5  2  10  Виведення  ?;  5) Введення: 2  6  7  9  Виведення  ?

Завдання 4. Самостійно скласти і реалізувати алгоритм впорядкування виразів: (1/k)+(1/m)-1/p)-(1/n); та (1/k)+(1/p)-(1/m)-(1/n) в порядку зростання для дробових чисел k,m,n,p.

Протестувати алгоритм на правильність на прикладах:

1)Введення    3  4  5  6  Виведення ? 2) Введення: 1  6  2 8 Виведення  ?; 3) Введення: 4  4  3 9 Виведення  ?;  4)Введення    6  5  2  10  Виведення  ?;  5) Введення: 2  6  7  9  Виведення  ?

Практична робота 2. 
Aлгоритми мовою Pascal

Завдання 1.  На конференцію приїхали рівно по k представників від m(не менше ніж 2) фірм-конкурентів по виробництву гри "Саmрf", при цьому, усі представники різних фірм є конкурентами. Відомо, що у кожного учасника конференції рівно  n конкурентів серед усіх інших учасників.  Скласти алгоритм, який знаходить найбільшу кількість учасників  та найменшу кількість фірм-конкурентів в конференції?

 Розв’язання.  Кількість учасників конференції дорівнює km осіб. З іншого боку, кількість конкурентів у одного представника дорівнює k(m-1)= n, звідси маємо рівність km =  n + k, права частина якого є лінійний вираз відносно двох змінних. Лінійний вираз р(k)= n + k досягає свого найбільшого і найменшого значення на межах числового проміжка від 1 до n. Якщо   k = n, то маємо найбільше значення р(n)= n + n =2n, тому  nm = 2n, звідси  m = 2. Відповідь: 2n осіб, 2 фірми.

Алгоритм мовою Pascal

program МіnConkurent;    var k,m,n:integer;    begin

writeln('введіть число конкурентів  в особи 2<n<10⁹  n='); readln(n);

write('найбільше:', 2*n, ' осіб');  {вивід найбільшого числа учасників}

write('найменше: 2 фірми'); {вивід найменшого числа учасників}

end.                              {оголошення кінця алгоритму}

Завдання 2.  На конференцію приїхали рівно по k представників від m(не менше ніж 2) фірм-конкурентів по виробництву гри "Саmрf", при цьому, усі представники різних фірм є конкурентами. Відомо, що у кожного учасника конференції рівно  n конкурентів серед усіх інших учасників.  Скласти алгоритм, який знаходить найбільшу кількість фірм-конкурентів і найменшу кількість представників в конференції?

 Розв’язання.  Кількість учасників конференції дорівнює km осіб. З іншого боку, кількість конкурентів у одного представника дорівнює k(m-1)= n, звідси маємо рівність km =  n + k, права частина якого є лінійний вираз відносно двох змінних. Лінійний вираз р(k)= n + k досягає свого найбільшого і найменшого значення на межах числового проміжка від 1 до n. Якщо   у формулі р(k)= n + k,  підставимо k = 1, то отримаємо найменше значення р(1)= n + 1 , тому найбільше значення m = n+1, звідси  n = m-1. Відповідь: n+1 фірм, 1 особа.

Алгоритм мовою Pascal

program МахConkurent;    var n:integer;    begin

writeln('введіть число конкурентів  в особи 2<n<10⁹  n='); readln(n);

write('найбільше:' n+1, 'фірм');  {вивід найбільшого числа фірм}

write('найменше: 1 представник від фірми'); {вивід найменшого числа представників }   end.   {оголошення кінця алгоритму}

Завдання 3. Відомо, що книжкова полиця вміщає k однакових товстих книг, але k+1-а книга вже не влазить. Так само на неї можна поставити m однакових тонких книг, а m+1 -а вже не влізе. Скласти алгоритм, який знаходить можливість, щоб на полиці помістилися одночасно: n товстих та p тонких книг.

Розв’язання.  Якщо числовий вираз  n/k + p/m <=1, то можна, якщо  числовий  n/k + p/m > 1, то не можна помістити одночасно книги на полицю.

Алгоритм мовою Pascal (використовує повне розгалуження, «якщо-то, інакше»)

program BIBLIO;    var k,m,n,p,h:real;    begin

writeln('введіть число товстих книг 2<k<10⁹  k='); readln(k);

writeln('введіть число тонких книг 2<m<10⁹  m='); readln(m);

writeln('введіть даних товстих книг 2<n<10⁹  n='); readln(n);

writeln('введіть даних тонких книг 2<p<10⁹  p='); readln(p);  h:=(n/k)+(p/m);

 if  (h<1) or (h=1) then write(' кнгиги можна помістити') {розгалуження для виводу результату}

else  write('не можна помістити книги');  {інакше то вивід результату не можна} writeln('h=', h); end.

Завдання 4. Самостійно скласти і реалізувати алгоритм впорядкування виразів: (n/k)+(p/m)-(m/p)-(k/m); та (р/k)+(n/m)-(k/n)-(n/p) в порядку зростання для дробових чисел k,m,n,p.

Завдання 5. Самостійно скласти і реалізувати алгоритм впорядкування виразів: (1/k)+(1/m)-1/p)-(1/n); та (1/k)+(1/p)-(1/m)-(1/n) в порядку зростання для дробових чисел k,m,n,p.

Практична робота 3. 

Нелінійні алгоритми 

Завдання 1. Є масив, що складається з N чисел. За один крок дозволяється зменшити на 1 кілька (можливо один) підряд рівних елементів. Мета – зробити всі елементи рівними нулю. За яку мінімальну кількість кроків це може бути зроблено? 

Формат введення-виведення:  Програма  зчитує з клавіатури (стандартного пристрою введення) натуральне число N (1≤N≤2∙10⁵) – кількість чисел у масиві, а з наступного рядка N невід’ємних цілих чисел, елементів масиву, кожне з яких не перевищує 2∙10⁹. Програма виводить на екран (стандартний пристрій виведення) єдине число – шукану кількість кроків.

PROGRAm Zeroing1;

type arr= Array[1..200005] of longint;

var  A: arr;      i, k, n: longint;

begin   read(n);    for i:=2 to n+1 do read(a[i]); writeln(' ****  n= ', n);  a[1]:=0;   k:=0;

  for i:=1 to n do   begin     writeln('*** a[',i,']=', a[i]); writeln(' a[',i+1,']=', a[i+1]);

    if a[i+1]>a[i] then k:=k+a[i+1]-a[i];   writeln(' k=', k);   end;

write(' Найменша кількість кроків  для обнулення елементів масиву  k=', k);  end.

Дані   для тестування алгоритму:  А)Введення: 3;  3; 4; 1; Виведення результату :  4.   

Б) Введення : 3; 3; 1; 4;  Виведення:  6.  В) Введення :  5; 4; 2; 5; 4; 4.  Виведення:  7.

Завдання 2. Є коло радіуса R з координатами центра  (х,у)  і пряма, що задана координатами двох своїх точок. Якої довжини відрізок прямої лежить всередині кола?

Вхідні дані. Задано рядок з 7-ми чисел: радіус кола, координати (х, у) центра і координати 2-х точок прямої. Всі числа цілі, за абсолютним значенням не перевищують 10000.

Вихідні дані. Вивести шкану довжину з точністю до 5 цифр після коми. Якщо коло і пряма не перетинаються, вивести -1, якщо дотикаються - вивести 0.

Розв'язання

Взаємне розташування кола і прямої має декілька випадків. Знаходимо відстань L  від центру кола до прямої, яка задана двома точками. Якщо відстань більша за радіус, то пряма і коло не перетинаються, коли ж рівні, то дотикаються, а інакше – слід знайти довжину хорди, яка сполучає дві точки перетину прямої і кола. Враховуємо, що відстань обчислена наближено. Для знаходження точок перетину прямої і кола – використаємо формулу.

PROGRAm CIRCUS2;

var r,x0,y0,x1,y1,x2,y2: integer;

a,b,c,aa,bb,cc,x3,y3,x4,y4,L,d,d1: real;

begin

readln(r, x0, y0, x1, y1, x2, y2);

L:=abs((x2-x1)*(y0-y1)-(y2-y1)*(x0-x1) )/sqrt(sqr(x2-x1)+sqr(y2-y1));

if (L-r)>0.00001 then writeln(-1)   else   if abs(L-r)<=0.00000005 then writeln(0)

else    begin    a:=y2-y1;   b:=x1-x2;   c:=x1*(y1-y2)+y1*(x2-x1);

if abs(b)<=0.000000001 then   begin   y3:=-sqrt(r*r-sqr(c/a+x0))+y0;

  y4:=sqrt(r*r-sqr(c/a+x0))+y0;      x3:=-c/a;      x4:=-c/a;

d:=sqrt(sqr(x4-x3)+sqr(y4-y3));   writeln(d:0:5);   end else  begin    aa:=a*a/(b*b)+1;   bb:=(y0+c/b)*a/b-x0;     cc:=x0*x0+sqr(y0+c/b)-r*r;

d1:=bb*bb-aa*cc; x3:=(-bb-sqrt(d1))/aa  x4:=(-bb+sqrt(d1))/aa; y3:=(-a*x3-c)/b;    

y4:=(-a*x4-c)/b;      d:=sqrt(sqr(x4-x3)+sqr(y4-y3));    writeln(d:0:5);    end;   end;   end.

Дані   для тестування алгоритму: 

А)Введення: 5 0 0 4 1 4 2  Виведення результату :  6.   

Практична робота 4. 

Нелінійні алгоритми геометричного змісту

Завдання 1. Cтворити та реалізувати алгоритм мовою Pascal, що визначає за  відомими довжинами трьох сторін трикутника чи має він внутрішній прямий кут.

PROGRAm LINEAR1;

var a,b,c,k: integer;

begin  readln(a, b, c);

while (a<>0)and(b<>0)and(c<>0) do begin      if c<a then   begin k:=c; c:=a; a:=k;

if c<b then begin k:=c; c:=b; b:=k; end; end;   if c<b then begin k:=c; c:=b; b:=k;

if c<a then begin k:=c; c:=a; a:=k; end; end;   if (a*a+b*b=c*c) then writeln(' yes')

else  if (a*a+b*b<>c*c) then writeln('nou');   writeln('    ', a, '    ', b, '    ', c);  end;  end.

Дані   для тестування алгоритму: 

А)Введення: 5  4   3   Виведення результату :  yes.   

Б)Введення: 5  12   13   Виведення результату :  yes.  

В)Введення: 25   24  7   Виведення результату :  yes.   

 Г)Введення: 5 4 6   Виведення результату :  nou.   

Завдання 2. Cтворити та реалізувати алгоритм мовою Pascal, що визначає за  відомими довжинами  a, b, c, d чи можна у прямокутник зі сторонами a, b цілком помістити прямокутник зі сторонами c, d.

Program fiercutnyk2;

const eps=0.000001;  var  a,b,c,d,hk,wk,hl,wl,ab,cd,bc,ad,af,ge,ga,ae,ac,cf,

bae, da, baf, bac, caf, cab, fac: real;   s:string;

begin   readln(a, b, c, d);

if a<b then  begin  wk:=b;  hk:=a;  end   else  begin  wk:=a;  hk:=b;  end;

if c<d then  begin  wl:=d;  hl:=c;  end   else   begin   wl:=c;   hl:=d;  end;

if hl>hk then s:='NO'   else   begin  if wk>=wl then s:='YES'  else  begin

ab:=wl; cd:=wl;  bc:=hl; ad:=hl;  af:=hk;   ac:=sqrt(wl*wl+hl*hl);

cf:=sqrt(ac*ac-hk*hk);  cab:=arctan(bc/ab);  fac:=arctan(cf/af);

bae:=3.1415926/2-cab-fac;  ge:=ad*sin(bae)+ab*cos(bae);

if (wk-ge)>=eps then s:='YES' else s:='NO';    end;  end;   writeln(s);   end.

Дані   для тестування алгоритму: 

А)Введення: 5  4   1  1   Виведення результату :  yes.   

Б)Введення: 5  8   1  3   Виведення результату :  yes.  

В)Введення: 25   24  3  5   Виведення результату :  yes.   

 Г)Введення: 5 4  6  8  Виведення результату :  nou.   

Завдання 3.  Cтворити та реалізувати алгоритм мовою Pascal, що визначає   координати вершини An  для правильного трикутника AnBnCn, якщо 

Program Tryangul;

var   an, a1, d, n,  x, y: real;    begin   readln(n);   a1:=1;    d:=2;   an:=a1+d*(n-1);

x:=(a1+an)*n/2-0.5-an/2;   y:=sqrt(3)*an/2;  writeln(x:0:3,' ',y:0:3);   end.

Дані   для тестування алгоритму: 

N= 20;  N= 25;   N= 50;  n=76

Довідковий матеріал про розгалуження

Розгалужений процес вміщує декілька шляхів. Вибір того чи іншого шляху залежить від виконання деяких умов. У багатьох випадках виникає потреба в зміні послідовного порядку операторів, що стає  можливим завдяки операторам управління. До них в першу чергу відносяться IF та CASE.

         Оператор IF реалізує операцію умовного переходу (операцію розгалуження на два напрямки).

Загальний вигляд:

If  умовний вираз  then…else…;

         В умовному виразі задається умова розгалуження. При виконанні оператора IF цей вираз обчислюється з отриманням логічного результату. Якщо результат True, то виконується простий або складний оператор після слова Then. Якщо результат False, то виконується оператор після Else.

         Наприклад:

If A<7.2 then Y:=5*A else Y:=5/A;

  Частину оператора Else … можна не вживати:

If X>0 then K:=K+1;

            Це означає, що у випадку, коли число Х більше нуля, буде виконано оператор K:=K+1. Якщо така умова для конкретного числа хибна, то змінення К не відбувається, а управління передається на оператор, який в програмі записано після оператора If.

         Складений оператор Begin…End суттєво розширює можливості If:

If X>0 then begin                    K:=K+1;                    R:=a;                   End          Else begin                   L:=L+1;                   Q:=A;                 End;

       

         У складному операторі записують будь-яку кількість операторів. Вони виконуються “як одне ціле”. Тут можуть бути “свої” If, цикли, тощо.

Зверніть увагу на те, що після оператора, який стоїть перед Else, не ставиться крапка з комою.

         Оператор Case забезпечує розгалуження на декілька напрямків.

         Загальний вигляд:

Case індекс вибору of список вибору;

Else…; End;

         де індекс вибору – проста змінна цілого, символічного, перелічуваного або логічного типу;

         список вибору – сукупність простих або складних операторів, перед кожним з яких стоїть константа вибору, тип якої співпадає з типом індексу вибору.

         Після слова Else може стояти простий або складний оператор (ця конструкція може бути відсутня).

         Приклад:

Case Kit of     1: Y:=sin(x);     2: Y:=cos(x);     3: Y:=sin(x)+cos(x);     Else Y:=0; End; {case}

        

         Змінна Kit (цілого типу) повинна бути визначеною до виконання оператора Case. Якщо Kit дорівнює 1, обчислюється функція Y:=sin(x), якщо вона дорівнює 2, то : Y:=cos(x). У тому випадку, коли Kit відрізняється від 1, 2 або 3, буде виконано оператор Y:=0.

         У списку вибору можна вживати складний оператор Вegin… End.

Приклад: скласти програму обчислення функції

Програма:

Var X, Y, Z, F : Real; Begin     Write(‘Введіть Y, Z :’);     ReadLn(Y,Z);     Write(‘Введіть X :’);     ReadLn(X);     IF (X>=Y) THEN  F:=SQR(X)+EXP(Z)/COS(Y)                      ELSE   F:=SIN(X)+COS(Z);     WriteLn(‘Значення F=’,F);             End.